آشوب، پیچیدگی و آنتروپی
گفتاری در فیزیک برای غیرفیزیکدانان
میشل بارنگر[1]
مرکز فیزیک نظری، آزمایشگاه فیزیک هستهای و دپارتمان فیزیک
موسسه تکنولوژی ماساچوست (MIT)، کمبریج، ماساچوست، امریکا
موسسه سیستمهای پیچیده نیوانگلند، کمبریج، ماساچوست، امریکا
(با سپاس از سرکار خانم الهه بابایی و آقای دکتر شروین ممتحن جهت برگردان و نگارش متن فارسی)
قرن بیستویکم با بانگ مهیبی آغاز گردید. این بانگ مهیب برای یک ذهن معمولی حاکی از انقلابی در تکنولوژی بود که میتوانست حتی انقلاب صنعتی قرون ۱۸ و ۱۹ را تحتالشعاع خود قرار دهد که داد و تا امروز نیز به تغییرات شگرفی در قوانین اقتصاد منجر شده است. اما برای افرادی با ذهن علمی، یک جنبه از این بانگ مهیب، به تحول بزرگی در موضوع "پیچیدگی" مربوط می شود که توانسته است کانون تحقیقات را در رشتههای مختلف علوم، همچون زیستشناسی انسانی و پزشکی تغییر دهد. اما علم فیزیک به عنوان پر سابقه ترین و سادهترین دانش بشری، چه نقشی در این تحولات باید ایفا کند؟ به عنوان یک فیزیکدان نظری، میخواهم تمرکزم را روی فیزیک نظری قرار دهم. آیا قرار است این دانش هم متحول شود؟
فیزیک نظری قرن بیستم از میان انقلاب نسبیت و انقلاب مکانیک کوانتوم سر برآورد و در مجموع، گویای سادگی و پیوستگی بود (علی رغم جهش های کوانتومی). ابزار اصلی آن، علم حساب[2] و آخرین نمود و دستاورد آن نیز تئوری میدان بود.
اما فیزیک نظری قرن بیست و یکم در حال سر بر آوردن از انقلاب آشوب است؛ درباره پیچیدگی سخن میگوید و ابزار اصلی آن کامپیوتر است. نمود نهایی آن هنوز مانده تا مشخص شود اما ترمودینامیک، به عنوان بخش محوری فیزیک نظری،تحت تاثیر این دگرگونی قرار خواهد داشت. (دورههای تئوری آشوب در آکادمی فیزیک ناصری)
آشوب
برای فیزیکدانان نظری، این انقلاب از چند دهه پیش با موضوع آشوب شروع شده است. آشوب یک مفهوم ریاضی محض و یک واقعیت انکار ناشدنی در ریاضیات است. میدانیم که فیزیک نظری بر پایه ریاضیات بنا شده و نیز اینکه تمام فیزیکدانهای نظری، ریاضیدانهای کاربردی هستند. پس اولین سوالی که میخواهم به آن بپردازم این است که چرا از میان تمامی متخصصین رشتههای علمی، علوم کاربردی، رشتههای مهندسی و علوم انسانی، فیزیکدانها باید عملاً آخرین نفراتی باشند که به موضوع آشوب علاقمند شوند و آن را در کارهای خود استفاده کنند؟ هرچند استثناهایی هم وجود داشته است. به عنوان مثال آنهایی که شتابدهندههای بزرگ ذرات را ساختند از آشوب مطلع بودند؛ در واقع آنها بودند که قسمت عمده موضوع را کشف کردند. استثناهای دیگری نیز وجود دارد. اما واقعیت این است که غالب فیزیکدانان چیزی درباره آشوب نمیدانستند، و هنوز هم نمی دانند. مهندسین رشتههای مختلف، هواشناسان، برخی از شیمیدانها، زیستشناسهای جمعیتی، متخصصین قلب، اقتصاددانها، و حتی روانشناسان، خیلی جلوتر از فیزیکدانان به آشوب مسلط شدهاند.
در طول دوران تدریسم در دانشگاه MIT، دو بار در قالب یک درس دوره کارشناسی رشته فیزیک، آشوب ساده را معرفی کردم. قصدم این بود که فیزیکدانهای آینده کشور در معرض موضوع آشوب قرار بگیرند. ولی در همان دانشکده فیزیک دانشگاه MIT، مدت مدیدی است که اعضای هیأت علمی، دیگر این درس را تدریس نمیکنند. آنها بعد از دو یا سه سال، شما را به سمت دیگری سوق میدهند تا مانع از به اصطلاح فسیلشدنتان شوند. و به همین ترتیب، شخصی که تدریس درس آشوب را بعد از من به عهده گرفته بود، دوبار آشوب را از برنامه آموزشی این رشته حذف کرد و در توضیح این کار اظهار داشت «با عرض پوزش، من چیزی درباره این جور چیزها نمیدانم و نمیتوانم آن را تدریس کنم.». باز باید بگویم استثناهای بزرگی هم وجود دارند ولی هنوز هم آشوب جزء برنامه درسی دانشگاههای عادی امریکا نیست؛ اکثر دانشجویان مدارک فیزیکشان را بدون این که در مورد آشوب چیزی شنیده باشند دریافت میکنند. در محبوبترین کتاب درسی مکانیک کلاسیک، هیچ مطلبی درباره آشوب وجود ندارد. نویسنده کتاب فروتنانه در مقدمه آن عذرخواهی میکند و میگوید موضوع آشوب به تنهایی کتاب کاملی را میطلبد، عذری بدتر از گناه! (دورههای تئوری آشوب در آکادمی فیزیک ناصری)
اما چرا اینطور است؟
پاسخ ساده است. فیزیکدانها هیچ گاه فرصت کافی برای آموختن آشوب نداشتند چرا که مسحور چیز دیگری بودند. آن چیز دیگر، همان فیزیک قرن۲۰ام بود! یعنی نسبیت، مکانیک کوانتوم و پیامدهای بیشمار آن دو. و البته علت دیگری را هم من اضافه می کنم: آشوب نه تنها برای آنها ناآشنا بود بلکه تا حدی هم به مذاقشان ناگوار میآمد! این را میگویم چون خود من هم همانطور بودم. چه چیزی از آشوب میتواند اینقدر ناگوار باشد؟ برای پاسخ به آن باید به چند صد سال پیش برگردم.
بیش از سه قرن پیش، نیوتن و لایبنیتس، تقریباً بطور همزمان، علم حساب را ابداع کردند و با انجام این کار، قدرتمندترین ابزاری که از زمان کشف اعداد تا به آن زمان میتوانست وجود داشته باشد را به زرادخانه ریاضی در دنیای علم تقدیم نمودند. یک روش برای اینکه وسعت علم حساب را درک کنیم این است که به آن از نظر هندسی نگاهی بیندازیم. قبل از ابداع علم حساب، هندسه میتوانست از پس بررسی خطوط مستقیم، صفحهها، دایرهها، کرهها و ترکیبهای مختلفی از آنها بربیاید. همچنین با کمی دشواری بیشتر بیضیها، سهمیها، هذلولیها و بیضویها، سهمویها، هذلولویها و شاید هم چند شکل پیچیدهتر را هم مطالعه کند و دیگر تمام. اما بعد از آمدن علم حساب، به طور مطلق هر نوع منحنی و هر نوع سطحی میتوانست بررسی و تحلیل شود به شرط آنکه به اندازه کافی هموار باشد.
ایده علم حساب، خودِ سادگی است. میتوان آنرا در چند جمله بیان کرد. بیایید تابع معلوم زیر را در نظر بگیریم:
y=f(x)
این نشانهگذاری بدین معنی است که اگر شما به من یک مقدار عددی معین را برای متغیر x بدهید، من یک مکانیزم (فرمول، برنامه کامپیوتری، آزمایش، یا چیز دیگری) در اختیار دارم که به من اجازه میدهد مقدار عددی y را بیابم: y بوسیله x معین میشود، y تابعی از x است، و ریاضیدانها مینویسند: y=f(x) همچنین اگر بخواهم میتوانم نموداری با استفاده از دو محور مختصات برای این تابع ترسیم کنم؛ محور افقی برای x و محور عمودی برای y. به ازای هر مقدار از x، من از مکانیزمی که در اختیار دارم استفاده میکنم و مقداری برای y پیدا میکنم تا نقطهای را بر روی نمودار بدست آورم. من این نمودار را با فرض اینکه یک منحنی هموار است در شکل ۱ کشیدهام و این منحنی را دوباره هم ترسیم کردهام.
در نمودار بالایی، تلاش کردهام به جای منحنی از قطعات نسبتاً بزرگی از خطوط مستقیم استفاده کنم که تصویر خیلی خوبی هم بدست نیامده. در شکل پایینی، همین کار را با استفاده از قطعات کوچکتری از خطوط مستقیم انجام دادهام که در نتیجه، تصویر بهتری ارائه شده است. اگر میخواستم از قطعاتی از این هم کوچکتر استفاده کنم، باز هم تصویر بهتری بدست میآمد. به نظرم شما هم با من موافق باشید اگر بگویم هر چقدر قطعات را کوچک و کوچکتر کنم، که ریاضیدانها به این فرایند «رفتن تا حد آخر[3]» میگویند، تقریب حاصله کامل و کاملتر خواهد بود. این تمام چیزی است که در علم حساب وجود دارد؛ در واقع کل درس همین است. هر چیز دیگری در علم حساب تنها بسط دادن همین ایده است.

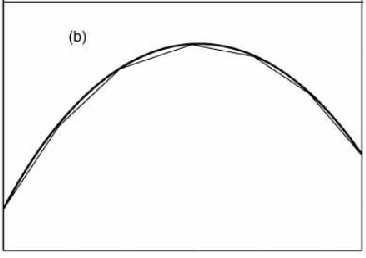
شکل (۱): اولین و آخرین درس حساب.
همانطور که میبیند، هموار بودن منحنی ضروری است، در غیر این صورت روش ما کار نمیکند. هموار بودن کلید کل کار است. منتها توابعی وجود دارند که برای ریاضیدانها به خوبی شناخته شدهاند اما هموار نیستند و بنابراین برای بررسی آنها نمیتوان از حساب استفاده کرد. ولی اگر خودتان را به توابع هموار محدود کنید، خواهید دید که هر کدام از آنها را بخواهید میتوان با هر درجهای از دقت، بوسیله قطعات خیلی کوچک از خطوط مستقیم تقریب زد و با توجه به اینکه ما همه چیزهایی را که باید درباره خطوط مستقیم بدانیم از قبل یاد گرفتهایم، در مورد منحنیهای هموار هم همه چیزی را که باید بدانیم میدانیم! تمام قدرت علم حساب در بسط دادن همین ایده است.
حداقل برای مدت ۲۰۰ سال، این ایده حساب، علم نظری را تغذیه کرده. ریاضیدانها مفاهیمی چون پیوستگی[4] و تحلیلپذیری[5] را برای توصیف دقیقتر هموار بودن ابداع کردند. کشف حساب منجر به انفجار اکتشافات بیشتری هم شد. شاخهای از ریاضیات بهوجود آمد که به نام تحلیل ریاضی[6] معروف است و نه تنها غنیترین شاخه در میان همه شاخههای ریاضی است بلکه با اختلاف، مفیدترین شاخه هم برای کاربردهای علوم کمّی[7]، از فیزیک گرفته تا مهندسی، از ستارهشناسی تا هیدرودینامیک و از علم مواد تا اقیانوسشناسی، میباشد. به این ترتیب دانشمندان نظری، ریاضیدانهای کاربردی شدند و ریاضیدانهای کاربردی افرادی هستند که تحلیل ریاضی، مانند کار با انتگرالها، معادلات دیفرانسیل، بسط سریها، نمایشهای انتگرالی توابع خاص و غیره در خونشان است. اینها ابزارهایی هستند که حساب فراهمشان کرده و قابلیت حل انواع مختلفی از مسائل را در تمام عرصههای علوم کمّی دارا میباشد.
بعد از گذشت چندین دهه موفقیت مداوم در استفاده از تحلیل ریاضی، ذهن نظریهپردازان از این تصور آکنده شد که تحلیل ریاضی، روش جهان ماست؛ اینکه همه مسائل، با فرض اعمال تلاش کافی و در اختیار داشتن قدرت محاسباتی کافی، نهایتاً قابل تحلیل خواهند شد. البته این اعتقاد در جایی بطور صریح اظهار نشد و تنها در ضمیرهای ناخودآگاه قرار داشت؛ ولی بیشتر علم قرن بیستم را به تسلط خود درآورد. این موضوع در انتخاب سر فصلهای دروس دانشگاهی و کتب درسی منعکس شده است. دو تئوری برجسته فیزیکی اوایل قرن بیستم یعنی نسبیت و مکانیک کوانتوم، هر دو به طور کامل از تحلیل ریاضی ریشه گرفتهاند. اما ایده شکستناپذیری تحلیل، قدرتمندتر از آن بود که در ضمیر ناخودآگاه باقی بماند. گویا مردم فراموش کردند که فرضهای اولیهای هم وجود دارند و بنابراین به مرور واقعیات مشروط به حقایق مطلق تبدیل شدند.
این را میگویم زیرا خودم هم تجربهاش کردهام. هیچ یک از ما فیزیکدانهای نظری حتی بر روی امکان وجود مسائل کاربردی که حساب در مورد آنها کارایی نداشته باشد بحث هم نمیکردیم. منحنیهای ناهموار، به عنوان «پدیدههایی پاتولوژیک» که تنها مورد علاقه ریاضیدانها هستند به شمار میآمدند. اگر به عمق این باور بروید آنچه در مییابید این خواهد بود که «همه چیز» میتواند به تکههای کوچکی از خطوط مستقیم تقلیل یابد، پس همه چیز را میتوان شناخت و فهمید به شرط آنکه در مقیاسی که به اندازه کافی کوچک است، مورد مطالعه قرار گیرد. حتی با اینکه ممکن است خیلی کار ببرد و گاهی هم ارزشش را نداشته باشد اما اصولاً ما دارای قدرت مطلق برای انجام این نوع تحلیل هستیم. بنابراین موفقیتهای بزرگ علم حساب، مسئول بخش مهمی از رویکرد تقلیلگرایی مجدانه در دانش قرن بیستم بوده است. رویکردی که به یک داشتن کنترل مطلق باور داشت؛ همان چیزی که حاصل دستیابی و احاطه بر جزئیات بود. گرچه ریاضیدانها از ابتدا به ما میگفتند که منحنیهای هموار فقط موارد استثنائی هستند و قانون نیستند؛ ولی ما گوش نکردیم!
آشوب، انقلاب ضد حساب
آشوب، کشف دوباره این نکته است که حساب قدرت نامحدودی ندارد. آشوب، در کلیترین معنای ممکن، مجموعهای از حقایق ریاضی است که ربطی به حساب ندارند و به همین دلیل است که به ذائقه فیزیکدانهای قرن بیستم ناگوار میآمد. از نظر کاربردی، تئوری آشوب طیف گستردهای از مسائل علمی و مهندسی را که به حساب پاسخگو نیستند حل میکند. این بدان معنا نیست که از این به بعد باید علم حساب را از مد افتاده در نظر بگیریم و همه توجهمان را به آشوب معطوف کنیم. خیر، علم حساب همه قدرت خود را حفظ میکند؛ ولی باید بدانیم که این قدرت محدود است. در واقع، حساب تنها جزيی از حقیقت است؛ یعنی یک عضو از یک زوج دوتایی است. آشوب عروسی است که از طرف ریاضیدانها برای ازدواج با آقای حساب انتخاب شده است! وقتی حساب برای اولین بار عروس آیندهاش را دید در اصل از او خوشش نیامد. ولی خب طلاقی هم در کار نخواهد بود؛ آن دو برای همیشه ازدواج کردهاند و در نهایت نیز حساب به شدت به آشوب علاقمند خواهد شد...!
در ادامه به طور خلاصه درباره اینکه آشوب چیست و چهطور با سیستمهای پیچیده انطباق مییابد توضیح خواهم داد. در میان تمامی ابعادی که برای بررسی موجودات فیزیکی استفاده میکنیم، فضا و زمان از همه مهمتر هستند. بیایید ابتدا آشوب در فضا را بررسی کنیم.
شیئی که در فضا به صورت آشوبناک است را «فرکتال» مینامند. برای واژه فرکتال تعاریف بسیاری وجود دارد. یک تعریف خیلی کلی این است که فرکتال شکلی هندسی است که وقتی آن را به اجزاء کوچک و کوچکتر تحلیل میکنیم سادهتر نمیشود. و البته بطور ضمنی بیانگر آنست که هموار هم نیست. ریاضیدانها از زمانهای بسیار دور، مثالهای سادهای از فرکتالها را میشناسند. مثلاً یک پارهخط مستقیم را در نظر بگیرید، آنرا به سه بخش تقسیم و بخش وسطی را حذف کنید. یک سوم وسط هر یک از دو پاره خط باقیمانده را نیز بردارید. یک سوم وسطی هر یک از چهار قسمت کوچکتر باقیمانده را نیز دوباره بردارید و به همین ترتیب تا بینهایت ادامه دهید. در وضعیت نهایی، شما یک فرکتال دارید که آنرا یک مجموعه کَنتُر[8] مینامند.
حال مثال مشابه دیگری از نوع دو بعدی را بیان کنیم. سطح درون یک مثلث متساویالاضلاع را در نظر بگیرید. سپس مثلث کوچکتری را در نظر بگیرید که با اتصال نقاط میانه سه ضلع مثلث اصلی بوسیله سه خط مستقیم بدست میآید. سطح مثلث دوم را از مثلث اول حذف کنید. شکل باقی مانده شامل سه مثلث است که در گوشه هایشان به هم میرسند و مساحت هر یک از آنها برابر با یک چهارم مثلث اصلی است. حال برای هر یک از این سه مثلث نیز همان کاری را که با مثلث اصلی کردید انجام دهید. و به همین ترتیب تا بینهایت ادامه دهید. اکنون شما فرکتالی دارید که به آن مثلث شِرپینسکی[9] میگویند (شکل ۲ را ببینید).

شکل (۲): مثلث شرپینسکی
(مرجع: بار-یام، دینامیک سیستمهای پیچیده).
بسیاری از مردم، از جمله خودم، قبلاً به چنین اشیائی به صورت یک سرگرمی ریاضی بدون ارزش کاربردی نگاه میکردند. اما ما بهخصوص از دهه ۱۹۷۰به این طرف چیز متفاوتی آموختیم. دو مثالی که ارائه کردم چیزهایی ابتدایی هستند، ولی این موضوع، در علم پیشرفت فراوانی داشته است و اکنون حالتهای بینهایتی برای تولید فرکتالها وجود دارد. مجموعه مشهور مَندلبرُت[10]، که برای استفاده در موزهها و کتابهای تصویری محبوبیت زیادی دارد، فرکتالی است کمی پیشرفتهتر که علیرغم پیچیدگیهای حاصله از آن، همچنان دارای تعریف به شدت سادهای است. خوبست این نکته را هم ذکر کنیم که پرینت گرفتن از یک فرکتال بر روی کاغذ غیرممکن است. تصویری که روی کاغذ میبینید تنها تقریبی از یک فرکتال واقعی خواهد بود. ولی در مورد مجموعه مندلبرت، حتی همین تقریب هم بسیار زیباست بهخصوص وقتی بهطور متوالی، بخشهای کوچک و کوچکتر آن را بزرگنمایی میکنید. برای فرکتالهای سادهتر مثل مجموعه کنتر و مثلث شرپینسکی، بزرگنماییهای متوالی، همیشه همان ساختار تکراری قبل را تولید میکند: به این نوع فرکتالها خود-متشابه میگویند. این امر اما در مورد مجموعه مندلبرت صادق نیست و بزرگنماییهای متوالی از آن، هر بار شگفتیساز و حیرتبرانگیز خواهد بود.
همه فرکتالها ساخته بشر نیستند. طبیعت پر است از فرکتالها. مثلا یک رشتهکوه یک فرکتال است. یک درخت کهنسال سالم یک فرکتال است. بدن انسان یک فرکتال است. الگوی سکونتگاههای بشری، برگی از درخت سرخس، الگوی گسلهای زلزله، آسمان در روزی نیمه ابری، ساحل انگلستان یا هر قسمت دیگری از ساحل، امواج روی سطح اقیانوس، الگوی پوشش گیاهی در صحرای سونوران[11] و ... همه اینها فرکتالهایی هستند با همان مفهوم کلی که در بالا ارائه شد؛ یعنی وقتی آنها را زیر میکروسکوپی هرچه قویتر بررسی کنید، سادهتر نمیشوند. برخی از آنها وقتی در مقیاسهای کوچکتر بررسی میشوند، عملاً درجه بالایی از خود-تشابهی را نشان میدهند.
به عنوان مثال میتوان به یک درخت، یک سرخس، یا یک رشتهکوه اشاره کرد. اما بقیه آنها، مثلاً بدن ما، اینطور نیستند؛ البته آنها را هم به گونهای که با علم حساب قابل بررسی باشند نمیتوان ساده کرد. ما در میان فرکتالها زندگی میکنیم. به هر حال زمانیکه فرکتالها دور و برمان باشند احساس بسیار راحتتری داریم تا وقتی که در میان اشکال اولیه کتاب هندسهمان باشیم. پس چطور است که واژه فرکتال تا قبل از سال ۱۹۷۴ هنوز ابداع نشده بود؟ آیا احتمالاً قدری ضدیت سیستماتیک با این موضوع وجود نداشته؟ در هر صورت اکنون سری کاملی از فرکتالها وجود دارند که توسط ریاضیدانها یا دانشمندان کامپیوتر ساخته شدهاند با این هدف که مشابه فرکتالهای طبیعی باشند. شما اغلب آنها را در برنامههای محافظ صفحه مانیتور و در بازیهای کامپیوتری یا در فیلمهای انیمیشن میبینید.
برای یک فیزیکدان مثل خودم، مثال مشهود دیگری نیز برای فرکتال وجود دارد که با طنز همراه است. ما در تمام طول قرن بیستم مشغول توسعه نتایج حاصل از مکانیک کوانتوم و نسبیت بودهایم، یعنی همان تئوریهایی که به شدت بر مبنای حساب پایهریزی شدهاند. مخصوصاً به شدت علاقمند بودیم این تئوریها را در مطالعه «ذرات بنیادی» به کار بگیریم و نتیجه قرار بود کشف قوانین بنیادی فیزیک و جهان باشد. در ابتدا، اتمها ذرات بنیادی بودند، همانطور که معنای یونانی کلمه اتم نیز به این موضوع دلالت دارد. ولی با مشاهده مقیاسهای کوچکتر متوجه شدیم در واقع خود اتمها از هسته و الکترونها تشکیل شدهاند و اینها تبدیل به ذرات بنیادی جدید شدند. پس از اینکه باز هم توانستیم مقیاس را کوچکتر کنیم، کشف کردیم که هسته از پروتنها و نوترونها، به علاوه جماعتی از فک و فامیل و سایر بستگان، ساخته شده است. پس دوباره تعریف ذرات بنیادی را عوض کردیم. چند دهه بعد، به لطف وجود شتابدهندههایی که انرژیشان روز به روز هم بالاتر میرود، میتوانیم در مقیاس حتی کوچکتری به جهان نگاه کنیم و اکنون میدانیم که در واقع ذرات بنیادی قدیمیمان از کوارکها با طعمهای مختلف و گلوئنها تشکیل شدهاند. آیا این فرآیند قرار است تا بینهایت ادامه داشته باشد؟ واقعاً دیگر دلیل خوبی برای اینکه به این سوال پاسخ «نه» بدهیم نداریم. فیزیک ذرات، یعنی حریم اندرونی علم حساب، خودش در واقع یک فرکتال بزرگ است و این فرکتال به مقدار نسبتاً زیادی دارای خاصیت خود-تشابهی است. شباهت بین طیفسنجی اتمی، طیفسنجی هستهای و طیفسنجی هادرونی (زیر هسته ای)، مثالی از این مدعاست.
بعد از صحبت درباره آشوب در فضا، بیایید آشوب در زمان را نیز در نظر بگیریم که در واقع دیدگاهی رایجتر درباره آشوب است و نیز جایی است که این کلمه از آنجا آمده است. به سیستمی که ترکیببندی[12] آن توانایی تغییر با گذشت زمان را داشته باشد یک «سیستم پویا[13]» میگویند. یک سیستم پویا از تعدادی «متغیر» و تعدادی «معادله حرکت» یا «معادله پویا» تشکیل شده است. متغیر میتواند هر چیزی باشد که بتواند با زمان تغییر کند. میتواند چندگانه یا تکی، و پیوسته یا گسسته باشد. متغیرها باید به گونهای انتخاب شوند که با اطلاع کامل از همه آنها بتوان «حالت» سیستم را در هر زمان مشخص، به صورت منفرد تعیین کرد. به عبارت دیگر، دو سیستم مشابه که مقدار همه متغیرهایشان یکسان باشد، هم در زمان حال دارای ترکیببندی همسان هستند و هم در ادامه مسیرشان به شکل همسان تکامل خواهند یافت. به مجموعه همه مقادیر محتمل از متغیرها یعنی مجموعه همه حالتهای ممکن سیستم، «فضای فازی[14]» میگویند.
حالت کنونی سیستم به مثابه یک نقطه در فضای فازی است. وظیفه معادلات حرکت این است که تعیین کنند این نقطه در ادامه چگونه حرکت میکند. با داشتن حالت کنونی سیستم در فضای فازی، این معادلات حرکت به شما خواهند گفت که چگونه حالت سیستم را در لحظهای بعد محاسبه کنید. این نقطه با گذشت زمان، یک «ترژکتوری[15]» یا یک «مدار[16]» را در فضای فازی ترسیم و توصیف میکند. اگر بدانید ترژکتوری را چگونه باید محاسبه کنید میتوانید بگویید که معادله حرکت آن را حل کردهاید. معمولاً حالت سیستم در یک زمان اولیه به شما داده میشود که به آن «شرایط اولیه» میگویند. سپس شما سعی خواهید کرد که ترژکتوری سیستم را پس از این شرایط اولیه محاسبه کنید.
از ویژگیهای آشوب در زمان چیزیست که به آن «حساس بودن به شرایط اولیه» میگویند. بر این اساس، اگر دو مجموعه از شرایط اولیه یا دو نقطه اولیه در فضای فازی را که بهشدت به یکدیگر نزدیک باشند داشته باشید، ترژکتوریهای حاصله با اینکه حرکت خود را در ابتدا کنار یکدیگر شروع کرده و ادامه میدهند، اما نهایتاً به صورت واگرا از یکدیگر دور خواهند شد. ادوارد لورنز[17]، کاشف موضوع حساسیت به شرایط اولیه، آن را «اثر پروانهای» نیز نامیده است چرا که بر اساس حساسیت به شرایط اولیه، اگر امروز پروانهای در یکی از جزایر دریای کارائیب بالهای خود را به هم بزند میتواند باعث تغییر کامل در الگوی آب و هوای ماه آینده در اروپا شود. اگر یک سیستم پویای دلخواه را با تعدادی معادله حرکت من درآوردی در نظر بگیرید، شانس زیادی خواهید داشت که حساس یودن به شرایط اولیه را در آن سیستم مشاهده کنید.
در این مورد، آشوب در زمان، بیشتر یک قانون است تا یک استثناء! در مکانیک کلاسیک، خلاف ویژگی "حساس بودن به شرایط اولیه" را ویژگی «انتگرالپذیری[18]» مینامند. یک سیستم انتگرالپذیر سیستمی «چند پریودی[19]» است یعنی میتواند بهوسیله مجموعهای از متغیرها که به طور پریودیک با زمان تغییر میکنند توصیف شود. این موضوع برای بیشتر سیستمهای ساده متداول مانند سیستم کپلر (تعامل دو جرم سماوی بر اساس گرانش نیوتنی) یا نوسانگر هارمونیک چندبعدی صدق میکند. در واقع این خاصیت برای تمام سیستمهایی که در اکثر کتب درسی مکانیک کلاسیک مورد بررسی قرار میگیرند، صادق است. آن کتب درسی این احساس را القاء میکنند که همه مسائل جالب دنیا باید انتگرالپذیر باشند در حالیکه سیستمهایی که در این کتابها مورد بحث قرار گرفتهاند مجموعهای نزدیک به تهی را در واقعیت تشکیل میدهند! به همین خاطر است که چندین نسل از دانشجویان تا به امروز گمراه شدهاند.
"حساسیت به شرایط اولیه" مرگ "تقلیلگرایی" است و در واقع بیانگر آنست که هر عدم قطعیت کوچکی که در شرایط اولیه وجود داشته باشد میتواند به صورت نمایی با زمان رشد کند و نهایتا (و در اغلب موارد خیلی زود) به حدی بزرگ شود که تمام دانش مفیدی که درباره حالت سیستم داشتیم از دستمان برود. حتی اگر اکنون حالت سیستم را با دقت بسیار بالا بدانیم، هرگز نخواهیم توانست ترژکتوری آینده را پیشبینی کنیم. هرچند میتوانیم این کار را برای مدت زمان کوتاهی انجام دهیم ولی خطا به صورت نمایی رشد خواهد کرد و در جایی بالاخره مجبور خواهیم شد کار را رها کنیم. این موضوع شما را به یاد پیشبینیهای هواشناسی نمیاندازد؟ البته که میاندازد! در واقع لورنز یک هواشناس بود.
بین آشوب در زمان و آشوب در فضا ارتباط تنگاتنگی وجود دارد. یک سیستم آشوبناک پویا را در نظر بگیرید. ناحیه سادهای مثل یک کره یا یک مکعب یا هر حجم ساده دیگری را در فضای فازی آن انتخاب کنید. فرض کنید این ناحیه، مکان هندسی تمام شرایط اولیه ممکن برای این سیستم باشد. حال اجازه دهید زمان به جریان افتد. همچنان که هر نقطه از این ناحیه ترژکتوری خود را طی میکند، خود ناحیه نیز حرکت میکند و تغییر شکل میدهد. ناحیه در طول سیر تکاملش، به آرامی اما با اطمینان به یک فرکتال تبدیل خواهد شد. این فرکتال با گذشت زمان کاملتر میشود و در زمان بینهایت تبدیل به یک فرکتال کامل خواهد شد. هر سیستم آشوبناک پویا یک ماشین تولید فرکتال است و بر عکس، هر فرکتال را نیز میتوان به صورت نتیجهای محتمل از حرکت بلند مدت آشوب در زمان در نظر گرفت.
یک جنبه از آشوب نیز وجود دارد که زمان زیادی طول کشید تا بتواند به فرهنگ علم حساب نفوذ کند. آن جنبه این است که آشوب میتواند یک ویژگی از سیستمهای خیلی ساده باشد. تا همین اواخر، به طور گسترده اعتقاد بر این بود که نوعی از پیچیدگی که امروزه آنرا در ارتباط با آشوب میدانیم و البته در جاهای مختلفی از جهان واقعی قابل مشاهده است، باید به علت وجود تعداد بسیار زیادی از متغیرهای مستقل باشد که در نتیجه، حل کردن چنین مسائلی به هر روشی مشکل است و این دلیلی برای عدم تمایل به پرداختن به این گونه پدیدههای «آشوبناک نما» بود: زیرا اینگونه مسائل را غیرقابل حل در نظر میگرفتند. اما این اعتقاد، کاملاً اشتباه از کار در آمد. برای یک جریان، یعنی یک سیستم پویا که در آن زمان به صورت پیوسته جریان دارد، تنها کافیست سه بُعد وجود داشته باشد تا آشوبناک شدن این سیستم در بخشی از فضای فازیاش با قطعیت رخ دهد. برای یک نگاشت[20]، یعنی موردی که در آن زمان با گامهای محدود تغییر میکند، وجود یک بُعد هم کافی است. مثال معروفی از سیستم نوع اول، سیستمی است که توسط لورنز بررسی شد: سیستمی مشتمل بر سه معادله ساده با سه متغیر. لورنز میخواست این سیستم را به عنوان مدلی برای آب و هوا ارائه کند، که البته باعث خنده برخی از مخاطبان نیز شد، اما در عوض، موضوع حساسیت به شرایط اولیه را کشف کرد. مثالی از سیستم نوع دوم، نگاشت لوجیستیک است که از زمانهای دور توسط زیستشناسان جمعیت برای مطالعه تغییرات فصلی در فراوانی گونهها استفاده میشده است. در واقع مشخصه ساده بودن آشوب، آنرا از پیچیدگی کاملاً متفاوت میسازد؛ و این نکتهایست که در ادامه به آن برخواهیم گشت.
وقتی برای اولین بار این ویژگی مهم آشوب، "که میتواند خصوصیتی از سیستمهای بسیار ساده باشد" و اغلب هم هست، را شنیدم به شدت شوکه شدم. اگر این را به زبان خودمانی ترجمه کنیم چنین خواهد شد: سوالات ساده معمولاً پاسخهای پیچیده دارند. یعنی شما یک سوال ساده میپرسید، و با داشتن چند معادله حرکت ساده و تعدادی شرط اولیه ساده، اما پاسخ مسئله که یک ترژکتوری در فضای فازی است، آشوبناک از کار در میآید! من مسلماً در طول تحصیلات کارتزینآلود خودم در فرانسه، آموخته بودم که سوالات ساده باید جوابهای ساده داشته باشند و هر چیزی غیر از این باشد، نازیبا، غیرمنطقی و غیرهنری است. اما همانطور که میبینید مجبور شدهام خودم را عوض کنم.
و اینکه جنبه دیگری از آشوب هم هست که با پیچیدگی مشترک است. در هر دو مورد، حرکت سیستم باید غیرخطی باشد. در این رابطه، خطی بودن بدان معناست که معادلات حرکت نباید دارای متغیری با توان بالاتر از ۱ باشند. در مسائل یک بُعدی، خطی بودن برابر است با اینکه بگوییم سیستم واکنشی متناسب با محرک از خود نشان میدهد. در صورتیکه هر توان دیگری در هر قسمتی از معادلات وارد شود، معادلات را غیرخطی میکند. معادلات خطی معادلاتی ویژه هستند و روشی عمومی برای حل دقیق تمامی آنها وجود دارد. آنها هرگز به آشوب منتهی نمیشوند. از زاویهای، ظاهرا بیاهمیت و پیش پا افتاده به نظر میرسند و از زوایهای دیگر، بسیار مفیدند، دقیقاً به این دلیل که میدانیم با آنها چه کار کنیم. بسیاری از پدیدههای ساده وجود دارند که در واقع از معادلات خطی بطور تقریبی پیروی میکنند. این پدیدهها از پاندول ساده، اگر دامنه نوسان آن خیلی بزرگ نباشد، گرفته تا انتشار نور در خلا را در بر میگیرد به شرط آنکه شدت نور زیاده از حد بالا نباشد (که تقریبا همیشه اینطور است). بنابراین شگفتآور نیست که فیزیکدانها در گذشته، مقدار بسیار زیادی از انرژی خود را صرف پرداختن به معادلات خطی و مقدار بسیار کمتری از آن را صرف معادلات غیرخطی کردهاند، علیرغم وجود این واقعیت که معادلات غیرخطی در جهان بسیار عمومی و شایعترند.
و اما غیرخطی بودن چهطور فرکتالها و آشوب را تولید میکند؟ برای این سوال یک و تنها یک جواب وجود دارد: کش آوردن و تا زدن[21]. همه جریانها و نگاشتهایی که فرکتال تولید میکنند این کار را به وسیله کش آوردن و تا زدن انجام میدهند. بیایید نگاهی به یک مثال ساده بیندازیم. شیرینیپزی را در حال پختن یک عدد کروسان[22] درنظر بگیرید. او خمیر را روی میز پهن کرده و آن را با وردنه کش میآورد. بعد یک لایه کره روی آن میگذارد و آن را تا میزند. او دوباره آن را پهن کرده و کش میآورد، لایه دیگری از کره رویش میگذارد و دوباره تا میزند و همینطور تا بینهایت یا چیزی در همین حدود! چیزی که بدست میآید، یک نان کروسان خوشمزه است که با لایههای بسیار زیاد (نزدیک به بینهایت)، یک فرکتال در جهت عمود بر زمین میباشد. این روش کار همه آشوبهای پویاست. در اینجا به سادگی میتوانیم ببینیم چهطور حساسیت به شرایط اولیه رخ میدهد. دو نقطه نزدیک به هم را در خمیر اولیه در نظر بگیرید. وقتی خانم شیرینیپز اولین بار خمیر را پهن میکند این دو نقطه از یکدیگر فاصله میگیرند مگر اینکه در راستای عمودی یکسانی باشند که البته بسیار نامحتمل است. دفعه بعد که او خمیر را پهن میکند آنها باز هم از یکدیگر دورتر میشوند. نهایتاً انتظار میرود در یکی از دفعات عملیات کش آوردن و تا کردن خمیر، آن دو نقطه ما در لایههای مختلفی از کروسان قرار گیرند. پس از آن دیگر هر کدامشان تاریخچه متفاوتی خواهند داشت و حتی اگر زمانی دوباره به یکدیگر نزدیک شوند و همدیگر را ملاقات کنند، صرفاً به دلیل تصادفی محض خواهد بود. همه این چیزها خیلی ساده و خیلی روشناند! ولی این برای فیزیکدانها در دهه ۱۹۷۰ موضوعی تازه بود. و البته خیلی خیلی مفید از کار درآمد. اما غیرخطی بودن کجای این ماجراست؟ در تا زدنها. درواقع معادلات خطی حرکت رفتارشان با تغییرات دامنه تغییر نمیکند. اگر کشیده شوند تا ابد کشیده میشوند ولی هرگز تا نمیخورند. این غیرخطیبودن است که تا میخورد.
این همه چیز در مورد آشوب بود. حال باید وارد سیستمهای پیچیده شویم.
به طور خلاصه دیدیم که آشوب رویای تقلیلگرایی ما را درهم شکست؛ رویایی که بر اساس آن اگر به قدر کافی درباره جزئیات میدانستیم، قدرت مطلق از آن ما بود. اما آشوب و حساب به یکدیگر نیازمندند و در کنار هم ثمرات فراوان به بار می آورند.
پیچیدگی
در حال حاضر، هنوز مفهوم پیچیده بودن یک سیستم به دقت توضیح داده نشده است که البته طبیعی است. به مرور که افراد، بیشتر و بیشتر بر روی سیستمهای پیچیده کار میکنند، فهم بهتری از ویژگیهای آن برای تعریفشان بدست میآورند. با این حال، تعریف این ایده در حال حاضر به نوعی مبهم و از نویسندهای به نویسنده دیگر متفاوت است. ولی توافق نسبتاً کاملی وجود دارد که سیستمهای پیچیده «ایدهآل»، یعنی آنهایی که ما بیشتر تمایل داریم درکشان کنیم، انواع زیستی[23] آنها هستند؛ مخصوصاً سیستمهایی که با انسانها سر و کار دارند از جمله بدنهای ما، گروههای ما، جامعه ما، و فرهنگ ما. حال که تعریف دقیقی از معنای پیچیدگی در دسترس نداریم، سعی میکنیم این مفهوم را با برشمردن ویژگیهایی تکمیل کنیم که به نظر میرسد عمومیترین ویژگیهای پیچیدگی باشند. بعضی از این ویژگیها در تعداد زیادی از سیستمهای غیر زیستی نیز وجود دارند:
۱-سیستمهای پیچیده دارای اجزای زیادی هستند که تعامل غیرخطی دارند.
به یاد آورید که غیرخطی بودن شرط ضروری برای آشوب است و اینکه تقریباً تمام سیستمهای غیرخطی که فضای فازی آنها دارای سه بعد یا بیشتر باشد، حداقل در قسمتی از فضای فازیشان، آشوبناک هستند. این بدین معنی نیست که تمام سیستمهای آشوبناک پیچیده هستند، ابدا اینطور نیست! اول از همه اینکه آشوبناک بودن با تعداد خیلی کمی از اجزای سازنده نیز رخ میدهد؛ ولی پیچیدگی اینطور نیست. به زودی به تفاوت عمده آشوب و پیچیدگی خواهیم پرداخت.
۲-اجزای یک سیستم پیچیده دارای وابستگی متقابل[24] هستند.
مثالی از وابستگی متقابل چنین است: نخست سیستمی غیرپیچیده را با تعداد زیادی اجزای تشکیلدهنده در نظر بگیرید، مثلاً گازی که در یک محفظه است. 10% از اجزای تشکیلدهنده آن یعنی مولکولهایش را از محفظه خارج کنید. چه اتفاقی میافتد؟ هیچ اتفاق قابل توجهی نخواهد افتاد! فشار یا حجم یا دما و یا همه آنها کمی تغییر میکنند. ولی در کل، گاز نهایی درست شبیه گاز اولیه است و مثل آن رفتار میکند. حالا همین آزمایش را روی یک سیستم پیچیده انجام دهید. مثلاً 10% از بدن یک انسان را از سیستم جدا کنید: مثلاً یک پای آن را قطع کنید! نتیجه خیلی تماشاییتر از گاز مورد مطالعه خواهد بود. من ادامه ماجرا را به شما واگذار میکنم. و البته توجه داشته باشید که من حتی عضوی مانند سر را برای جدا کردن پیشنهاد ندادم.
۳-یک سیستم پیچیده، ساختاریست که در برگیرنده اشل های متعدد است.
دوباره مثالهایی از بدن انسان را در نظر بگیرید:
اشل ۱: سر، تن، لبها، . . .
اشل ۲: استخوانها، عضلات، معده، خون، اعصاب، . . .
اشل ۳: سلولها، و هر کدام دارای هسته، میتوکندری، سیتوپلاسم، . . .
اشل ۴: کروموزومها شامل DNA، ملکولهای پروتئین تخصصی، هر کدامشان نقش خاصی بر عهده دارند . . .
در هر اشلی میتوان به یک ساختار جدید دست پیدا کرد و این ویژگی حتمی و جدید سیستمهای پیچیده است که ما را به ویژگی چهارم این سیستمها میرساند . . .
۴-یک سیستم پیچیده قادر به رفتارهای نوپدید[25] است.
پدیدآیی[26] هنگامی رخ میدهد که توجه خود را از یک مقیاس (اشل) به مقیاسی بزرگتر در بالای آن متمرکز کنیم. یک رفتار خاص که در مقیاسی معین مشاهده میشود را در نظر بگیرید. این رفتار خاص، درصورتی یک رفتار نوپدید تلقی میگردد که چنانچه هر یک از اجزاء آن اشل را بطور جداگانه و یک به یک مطالعه کنید نتوانید آن رفتار خاص را درک کنید؛ اجزائی که خودشان هم میتوانند یک سیستم پیچیده در مقیاسی کوچکتر باشند. بنابراین رفتار نوپدید، رویدادی است مخصوص به اشل مورد نظر که از تعاملات سراسری بین اجزای سازنده سیستم در همان اشل حاصل شده است. به عنوان مثال بدن انسان قابلیت راه رفتن دارد. این یک ویژگی نوپدید در بالاترین مقیاس است که در بالا به آن اشاره شد. اگر تنها یک سر، یک تنه، یا یک پا را مطالعه کنید هرگز راه رفتن را درک نخواهید کرد.
ترکیبِ داشتن ساختار و پدیدآیی، به خودسازماندهی[27] منجر میشود. خودسازماندهی زمانی اتفاق میافتد که یک رفتار نوپدید بر تغییر ساختار و یا خلق ساختاری جدید تاثیر داشته باشد.
دسته خاصی از سیستمهای پیچیده وجود دارند که به طور خاص برای سازگاری با موجودات زنده ساخته شدند. به آنها سیستمهای پیچیدهی تطبیقپذیر[28] گویند. همانطور که از نامشان پیداست، آنها توانایی این را دارند که برای انطباق با محیطی در حال تغییر، خودشان را تغییر دهند. آنها همچنین میتوانند محیطشان را نیز برای اینکه برای زیستشان مناسبتر شود تغییر دهند. در این میان، دسته محدودتری هم وجود دارند که خودبازتولید[29] هستند: آنها تولد، رشد و مرگ را میشناسند. راجع به این سیستمها خیلی کم میدانیم که آن هم اطلاعاتی بسیار کلی است و به عنوان موضوعات انتزاعی تئوریک در نظر گرفته میشوند.
ما درباره زیستشناسی چیزهای زیادی میدانیم ولی در مورد انواع دیگر جنبههای زیستی، یا به طور کل، زندگی چیز زیادی نمیدانیم، آن هم اگر بتوان ادعا کرد که اصلاً چیزی میدانیم. ولی افرادی هستند که روی این موضوع کار میکنند که بسیار جذاب است.
حال بیایید دوباره به ارتباط بین پیچیدگی و آشوب برگردیم. گفتیم که آنها به هیچ وجه یکی نیستند. وقتی به یک فرکتال ریاضی ابتدایی نگاه میکنیم، ممکن است خیلی «پیچیده» به نظر برسد، ولی این پیچیده بودن به معنای آن پیچیدگی که وقتی از «سیستمهای پیچیده» صحبت میکنیم نیست. یک فرکتال ساده آشوبناک است ولی پیچیده نیست. مثال دیگر میتواند همان مثال گاز سادهای که به آن اشاره شد باشد: آن گاز به شدت آشوبناک است ولی بر اساس مفهومی که اکنون میشناسیم پیچیده نیست. پیش از این دیدیم که پیچیدگی و آشوب هر دو دارای ویژگی مشترک غیرخطی بودن هستند. از آنجایی که عملاً تمام سیستمهای غیرخطی در زمانهایی آشوبناک هستند، بدان معناست که وجود پیچیدگی، بطور ضمنی دلالت بر حضور آشوب دارد. اما برعکس این موضوع درست نیست.
آشوب موضوع بسیار بزرگی است. مقالات بسیاری در این زمینه نوشته شده و قضیههای بسیاری ثابت شدهاند. ولی پیچیدگی خیلی خیلی بزرگتر است. پیچیدگی مشتمل بر ایدههای فراوانی است که ربطی به آشوب ندارد. آشوب اساساً ریاضیات محض است و تاکنون نسبتاً به خوبی شناخته شده است. پیچیدگی اما هنوز تقریباً به کلی ناشناخته است. پیچیدگی در واقع ریاضیات نیست. بیشتر فیزیک نظری یا هر چیز دیگر نظری است. البته در حالت خوش فرمش، بسیار از ریاضی و احتمالا ریاضیات جدید استفاده خواهد کرد.
بنابراین موضوع آشوب زیرمجموعه بسیار کوچکی از موضوع پیچیدگی است. احتمالاً برجستهترین تفاوت بین این دو، چیزی باشد که در ادامه توضیح میدهم: یک سیستم پیچیده همیشه دارای اشلهای متعدد است. چنانچه آشوب مثلا بر اشل n یک سیستم حکمفرما باشد، اشل قبلی (یعنی مقیاس n-1) ممکن است در وضعیت خودسازمانده (self-organiser) باشد که به معنایی نقطه مقابل آشوب است. بر این اساس میتوانیم مورد پنجم را به لیست ویژگیهای سیستمهای پیچیده اضافه کنیم:
۵-پیچیدگی دربرگیرنده تعاملی متقابل بین آشوب و غیر آشوب است.
افراد زیادی معتقدند که پیچیدگی «در آستانه آشوب» رخ میدهد، ولی کسی تا بهحال نتوانسته این موضوع را بطور کامل توضیح دهد. معنی آن از قرار معلوم چیزی است که در ادامه خواهد آمد:
تصور کنید معادلات حرکت شامل چند پارامتر «کنترل» باشند که میتوانند بسته به محیط تغییر کنند (مثال: دما، غلظت، یا شدت تاثیری خارجی مثل نورخورشید). میدانیم که بیشتر سیستمهای غیرخطی، 100% آشوبناک نیستند: آنها برای مقادیری از پارامتر کنترلشان آشوبناک و برای بقیه مقادیر آن غیر آشوبناک هستند. پس آستانهای برای آشوب وجود دارد که برابر است با مقدار دقیقی از پارامتر کنترل که در آن، ماهیت عناصر دینامیکی سیستم عوض میشود. این اتفاق همچون نقطهای بحرانیست که در عبور فاز سیستم از ماهیتی به ماهیت دیگر رخ میدهد. نقطهای که در آن ارتباطات بلندمدت اهمیت زیادی دارند. شاید سیستمهای پیچیدهای مانند سیستمهای بیولوژیکی، بتوانند محیطشان را به گونهای تغییر دهند که تا حد ممکن در موقعیت آستانه آشوب به کار خود ادامه دهند. این موقعیت در واقع جایگاهی است که در آن، بیشترین احتمال خود-سازماندهی وجود دارد. اینکه انتظار داشته باشیم ویژگی خود-سازماندهی موقعی ایجاد شود که روابط بلندمدت قوی بین اجزا وجود داشته باشد بسیار با عقل جور در میآید.
در نهایت ویژگی دیگری در سیستمهای پیچیده وجود دارد که همه ما را به شدت نگران میکند و از طرف دیگر جذابیت خاصی به آن میدهد. این موضوع در واقع توجه تمام سیستمهای اجتماعی یعنی تمام مجموعههایی که از قوانین تکامل پیروی میکنند را به خود معطوف میسازد. مثالهایی در این مورد عبارتند از: جمعیتهای گیاهی، جمعیتهای حیوانی، گروهبندیهای اجتماعی، سیستم ایمنی بدن ما، و نیز گروههای انسانی در اندازههای مختلف مانند خانواده، قبیله، شهر - ایالتها، طبقات اجتماعی یا اقتصادی، تیمهای ورزشی، و البته جوامع مدرن و شرکتهای بینالمللی. همگی برای تکامل یافتن و زنده ماندن، و البته پیچیده باقی ماندن باید از قانونی که در ادامه میآید پیروی کنند:
۶- پیچیدگی دربرگیرنده تعاملی متقابل بین همکاری[30] و رقابت[31] است.
طبعا این هم تعاملی متقابل بین اشلهاست. وضعیت عادی این است که رقابت در اشل n از همکاری در اشل کوچکتر قبل از خود (مقیاس n+1) تغذیه میشود. کولونیهای حشرات مانند مورچهها، زنبورها یا موریانهها، نمایشی تماشایی از این موضوع را ارائه میکنند. بهعنوان مثالی جامعه شناختی، خانوادههای طبقه متوسط اجتماعی در قرن نوزدهم را که توسط جین آستن[32] یا هونوره دبالزاک[33] توصیف شدهاند در نظر بگیرید. آنها با هدف موفقیت اقتصادی و برای بهدست آوردن مطلوبترین همسران برای جوانانشان با یکدیگر رقابت میکردند. آنان در صورتی بیشتر موفق میشدند که از همکاری و وفاداری بیدریغ اعضایشان برخوردار میبودند و نیز درصورتیکه تمام اعضایشان فرصت شرکت کردن در تصمیمگیریها را پیدا میکردند. مثال بعدی جنگ بین ملتها و میهنپرستی ملتهایی است که میتواند به آن دامن بزند. زمانیکه این دوگانه رقابت-همکاری را درک کنیم میتوان ادعا کرد که از کلیشه قدیمی «بقای اصلح[34]» و آسیبی که به مفهوم تکامل در ذهن عموم وارد آورده است، فاصله درست و حسابی گرفتهایم.
آنتروپی
بدیهی است که مطالعه سیستمهای پیچیده، مستلزم استفاده از بعضی انواع روشهای آماری میباشد. برای این کار باید از مکانیک و همزمان از آمار استفاده کنیم که به آن مکانیک آماری[35] میگویند. ولی نام دیگری هم برای مکانیک آماری وجود دارد که ترمودینامیک است. ترمودینامیک درباره انرژی آشفته است. مقدار زیادی از این نوع انرژی در سیستمهای پیچیده وجود دارد: فقط دو سیستم پیچیده معروف یعنی آب و هوا و اقتصاد را در نظر بگیرید. ترمودینامیک درباره درک ارتباط بین انرژی آشفته و انرژی منظم است. در فیزیک و شیمی، انرژی کاملاً آشفته را گرما میگویند. و پیشوند ترمو- هم از واژهای یونانی به معنای گرما آمده است. عنوان ترمودینامیک توسط فیزیکدانانی که با دیدگاه تجربی در اواسط قرن نوزدهم روی این مسائل کار میکردند ارائه شد. عنوان مکانیک آماری مربوط به فیزیکدانان جدیدتر است که با دیدگاه تئوریک، آن مسائل را مطالعه میکنند و در تلاش هستند تا قوانین ترمودینامیک را با استفاده از آمار از مکانیک بدست آورند.
معمولاً افراد غیرمتخصص، به خوبی میدانند که انرژی چیست. چه منظم باشد یا نباشد. بنابراین آنها مشکلی با فهم قانون اول ترمودینامیک یعنی قانون بقاء انرژی ندارند که میگوید انرژی کل، مجموع انرژی منظم و آشفته است که مقدار آن ثابت است یعنی مقدار عددی انرژی کل با زمان تغییر نمیکند. ولی وقتی به قانون دوم ترمودینامیک میرسیم معمولاً افراد دچار مشکل میشوند. احتمالا به این خاطر که تعریفهای زیادی برای قانون دوم وجود دارد و اگر هر دو این تعریفها را کنار هم بگذارید، اغلب اینطور به نظر خواهد رسید که در مورد دو چیز کاملاً متفاوت سخن میگویند. این تعریفها اغلب شامل مفاهیمی هستند که ظاهر تکنولوژیکی دارند مثل واژه آنتروپی که تنها یک واژه تجملی برای «بینظمی[36]» است.
آنتروپی کمٌیتی است برای اندازهگیری این مفهوم شدیداً عامیانه. در واقع هر کسی قانون دوم را به طور ذاتی میداند. این قانون درباره نظم در مقایسه با بینظمی است. توضیح سادهای برای فهم آن وجود دارد که توضیح دقیقی هم هست و در ادامه میآید؛ توضیحی درباره تکوین یک سیستم ایزوله، یعنی سیستمی بدون هر نوع تعامل یا اتصال با بقیه جهان: تکوین خودبهخودی یک سیستم ایزوله هرگز نمیتواند منجر به کاهش آنتروپی (بینظمی) آن شود. آنتروپی همواره و تا زمانی که سیستم در حال تکامل باشد افزایش مییابد. اگر نهایتا این سیستم به تعادل برسد و دیگر تکامل نیابد، آنتروپیاش ثابت میشود.
به عبارت دیگر یک سیستم ایزوله که از هر کمک بیرونی محروم است، از به نظم درآوردن امورات خود عاجز است. در بهترین حالت میتواند اجازه دهد بینظمیاش به آرامی افزایش یابد. در بدترین حالت، بینظمی به سرعت پیشرفت میکند تا جایی که فراگیر شود که حالت تعادل یا وضعیت حداکثر آنتروپی است. همه کسانی که کودکی دوساله داشتهاند کاملاً با این معنا از قانون دوم آشنا هستند.
میبینیم که با توجه به نکاتی که گفته شد، برای یک سیستم پیچیده در حال تکامل که ایزوله است، آنتروپی که یک ویژگی از حالت کنونی سیستم میباشد، هرگز با گذشت زمان کاهش نمییابد. ممکن است ثابت بماند ولی این تنها تحت شرایط ایدهآل، که هرگز در عمل مشاهده نشده اتفاق میافتد. در جهان واقعی، آنتروپی همواره در حال افزایش یافتن است. بنابراین تکوین چنین سیستمی همواره بازگشتناپذیر است: اگر شما یک تکامل مشخص از سیستم خودتان را مشاهده کرده باشید، میدانید که تکامل برگشتی، یعنی ترتیبی که با معکوس شدن زمان اتفاق میافتد، هرگز امکانپذیر نخواهد بود، چرا که مستلزم کاهش آنتروپی در زمان خواهد بود. و این مانند شوک بزرگی است؛ زیرا در مکانیک هر حرکت ممکنی در جهت معکوسش نیز امکانپذیر است. درصورتیکه قانون دوم میگوید در مورد ترمودینامیک این قضیه هرگز صادق نیست. یعنی برای یک سیستم ایزوله، هیچ حرکت ترمودینامیکی هرگز بازگشتپذیر نخواهد بود. این درست برعکس چیزی است که در مکانیک رخ میدهد! اما چهطور چنین چیزی ممکن است در حالیکه گفتیم ترمودینامیک همان مکانیک بعلاوه آمار است؟
من باقی مقاله را به توضیح درباره این پارادوکس (برگشتناپذیری ترمودینامیک و برگشتپذیری مکانیک) که گاهی اوقات به آن «پارادوکس پیکان زمان[37]» میگویند و استنتاج قانون دوم اختصاص خواهم داد. آن هم به سادهترین شکل و در بنیادیترین سطح، درست شبیه آنچه در بحث قبل درباره علم حساب داشتیم. خواهید دید که وجود آشوب برای قانون دوم ضروری است. اگر آشوب وجود نداشته باشد قانون دوم وجود نخواهد داشت. اولین شخصی که این ارتباط را تشخیص داد یک جوان روسی به نام نیکولای کرایلف[38] بود. او در طول جنگ جهانی دوم یک دانشجوی تحصیلات تکمیلی در لنینگراد بود و در زمانی که در حین ماموریت دفاع هواییاش به هواپیماهای آلمانی مینگریست به این موضوع هم فکر میکرد. او کمی بعد در سن ۲۹سالگی به دلیل بیماری فوت کرد اما نامش برای همیشه همراه با ارتباط بین آشوب و ترمودینامیک باقی خواهد ماند.
در اینجا بهتر است توجه خواننده را به این نکته معطوف کنم که قرار است در مورد نوعی از آشوب صحبت کنیم که با آنچه اکثر مردم میشناسند متفاوت است. مهمترین نوع آشوب در بحثهای کاربردی، «آشوب مستهلک شونده[39]» نامیده میشود. ما میتوانیم به آن آشوب مهندسان نیز بگوییم. این نوعی از آشوب است که در آن «استرنج اترکتور[40]» وجود دارد. از طرف دیگر، نوع دیگری از آشوب که باید آنرا مجزا کنیم «آشوب پایسته[41]» است که همان آشوب فیزیکدانان خواهد بود. این همان آشوبی است که وقتی کسی با مکانیک کلاسیک، تئوری میدان کلاسیک، یا هر رشته دیگری کار کند که از مکانیک همیلتونی و هندسه سیمپلکتیک[42] خاص آن و انواع قوانین جالب بقاء بدست میآید، با آن مواجه خواهد شد. مثل همیشه، فیزیکدانها تمایل دارند از بنیادیترین دیدگاهها، یعنی «از زاویه اولین اصلها» به موضوعات نگاه کنند. آشوب پایسته دارای استرنج اترکتور نیست اما فرکتالهای دیگری دارد که درست به همان اندازه زیبا هستند.
در اینجا لازم است فضای فازی که پیش از این تعریف کردیم را دوباره مرور کنیم. ترمودینامیک تنها با سیستمهای بزرگ مشتمل بر اجزای زیاد سر و کار دارد. در غیر این صورت بین انرژی منظم و گرما نمیتوان تفکیک قائل شد. از این رو، فضای فازی باید دارای تعداد ابعاد زیادی باشد. سیستم مورد مطالعه میتواند پیچیده باشد یا نباشد و این موضوع ربطی به درستی قانون دوم ندارد. اگر حالت سیستم را به دقت میدانستیم قادر بودیم آن را به وسیله یک نقطه در فضای فازی بیان کنیم. اما واضح است که برای یک سیستم چند جزئی نمیتوان مکان این نقطه را به طور دقیق تعیین کرد. بنابراین ما تنها معلوماتی ناقص در اختیار داریم و میتوانیم آن را به وسیله یک توزیع بر مبنای احتمالات در فضای فازی بیان کنیم. مثلاً فرض کنید میدانیم نقطهای که بیانگر حالت سیستم است در جایی درون حجم معین در فضای فازی قرار دارد ولی نمیدانیم در کجای این حجم. پس میتوانیم معلومات ناقص خود را با استفاده از یک توزیع یکنواخت احتمالاتی که حجم را پر میکند و احتمال آن برای هر نقطه خارج از این حجم برابر صفر است نشان دهیم (شکل ۳ را ببینید). این البته مرسومترین مثال توزیع بر مبنای احتمالات نیست اما برای بیان هدف فعلی ما مناسب است.

شکل ۳: مثالی از معلومات ناقص.
در مرحله بعد، یک عدد را تعریف میکنیم که بیانگر «مقدار اطلاعات»ی باشد که درباره حالت سیستم میدانیم. مثلاً اگر آن احتمال به طور یکنواخت در تمام فضای فازی توزیع شده باشد، در آن صورت ما هیچ چیزی درباره حالت سیستم نمیدانیم و مدار اطلاعات برابر صفر است: I=0 اگر فضای فازی را به دو قسمت مساوی تقسیم کرده باشیم و بدانیم کدام یک از این دو قسمت، حالت سیستم را در خود دارد، در آن صورت، به زبان کامپیوتر، مقدار اطلاعات باید برابر یک بیت باشد، I=1 bit چرا که انتخاب ما انتخابی دودویی است: یا در این نیمه است یا در نیمه دیگر. حال اگر هر نیمه را دوباره به دو قسمت مساوی تقسیم کنیم و اگر بدانیم که حالت سیستم در کدامیک از این چهار ربع قرار گرفته، آنگاه اطلاعات باید دو بیت باشد: I=2 bits چرا که ما دو انتخاب دودویی انجام میدهیم. و به همین ترتیب الی آخر.
تعمیم این روند را میتوان با یک فرمول ساده بیان کرد. اگر احتمال وقوع حالت سیستم به طور یکنواخت در یک حجم V در فضای فازی توزیع شده باشد و اگر Z حجم کل فضای فازی باشد، آنگاه مقدار اطلاعات (در واحد بیت) برابر است با I = log (Z/V)، که در آن لگاریتم در مبنای ۲ محاسبه میشود. برای توزیعهای احتمالاتی پیچیدهتر، فرمول عمومیتری نیز وجود دارد ولی ما فعلا به آن نیازی نخواهیم داشت. توجه داشته باشید که بیت، واحدی نیست که از جرم، طول یا زمان ساخته شده باشد بلکه اطلاعات، کمیتی بیبعد است.
حال کمیت دیگری را که توصیف کننده مشخصه دیگری از توزیع احتمالاتی است تعریف میکنیم و آن «آنتروپی» توزیع احتمالاتی است که آنرا با نشان میدهیم. آنتروپی فقط معیاری برای کمبود اطلاعات ماست. بنابراین آن را به صورت زیر تعریف میکنیم:
I - مقدار ثابت = S
مقدار ثابت در رابطه فوق خیلی مهم نیست چرا که برای ما تغییرات آنتروپی مهم است نه خود آنتروپی. در مکانیک کوانتوم این ثابت دارای مقدار معینی است ولی آن را اینجا مورد بحث قرار نمیدهم. واحد S هم مانند واحد I است ولی علامتاش را معکوس کردهایم، پس میتوانیم آن را «تیب» (برعکس بیت) بنامیم. S نیز مانند I بیبعد است. (توجه داشته باشید که واحد متداول برای S دارای بعد است ولی این به آن دلیل بوده است که ترمودینامیککارها یک ضریب اضافه بعددار یعنی ثابت بولتزمن را به این فرمول اضافه کرده بودند). برای موردی که احتمال ما به طور یکنواخت در V توزیع شده است، فرمولی که برای I داشتیم به فرمول زیر برای S تبدیل خواهد شد.
ثابتی دیگر + I= log V
دوباره تکرار میکنم که آنتروپی معیاری از کمبود اطلاعات ماست. اگر تنها بدانیم که نقطهای که بیانگر حالت سیستم در فضای فازی است داخل یک حجم از این فضا قرار دارد اما دقیقا ندانیم کجای این حجم، آنگاه این نقطه میتواند هر کدام از تعداد بسیار زیاد (در واقع بینهایت) نقاطی باشد که در درون حجم هستند. بنابراین تعداد بسیار زیادی از حالات ممکن برای این سیستم وجود دارد و ما نمیدانیم که در واقع کدامیک از آنها درست است. این همان تعداد بسیار زیاد احتمالات شناختی است که بهوسیله کمیتی که آن را آنتروپی میخوانیم اندازهگیری میشود. وقتی میگوییم آنتروپی معیاری از بینظمی است، این بینظمی در ذهن ماست و در دانشی که ما از اوضاع داریم. کلمه توصیفی «بینظم» مانند کلمه توصیفی «رندم» همواره در جایی استفاده میشود که مقایسهای بین یک موقعیت یگانه، ایدهآل و مشخص با یک موقعیت واقعی -که ما آن را تنها یکی از بسیار احتمال ممکن میدانیم ولی نمیتوانیم هیچکدام از آنها را حذف کنیم- انجام میگیرد. اسباببازیهای کودک دو ساله باید سر جایشان به طور منظم در جعبه و کمد قرار گیرند ولی در عوض در جاهایی پخش شدهاند که مختصات دقیق آنها ارزش توجه یا ثبت کردن را ندارد.
حال که آنتروپی را تعریف کردهایم، سوال بعدی این است که چگونه آنتروپی به صورت تابعی از زمان تغییر میکند. حالات سیستم در فضای فازی آن منطبق با ترژکتوریهای مکانیک کلاسیک تکامل مییابند. هر یک از این احتمالات، با حالتی که به آن تعلق دارد متناظر خواهد بود. بنابراین توزیع احتمالاتی هم با زمان تغییر میکند. اما چه بر سر آنتروپی خواهد آمد؟ جواب خیلی ساده است و همچنین خیلی شوکآور. آنتروپی ثابت باقی میماند، اصلا تغییر نمیکند! برای حالت خاصی که در آن احتمال به صورت یکنواخت در حجم V توزیع شده باشد به راحتی میتوان این موضوع را مشاهده کرد. با گذشت زمان، این حجم تکامل می یابد، حرکت میکند و شکلش تغییر مییابد. اما بر اساس قضیه بسیار مهمی در مکانیک کلاسیک با عنوان قضیه لیوویل[43]، مقدار عددی این حجم هرگز تغییر نمیکند و عدد ثابتی برای حرکت است. و بنابراین آنتروپی هم ثابت است، چرا که آنتروپی در واقع تنها logV است. پس حالا به این تناقض وحشتناک رسیدهایم. از طرفی قانون دوم میگوید آنتروپی باید با زمان افزایش یابد مگر در وضعیتهای تعادل، و از طرف دیگر قضیه لیوول میگوید آنتروپی هرگز نمیتواند تغییر کند. این پارادوکس دلیل اصلی این است که چرا آنتروپی چنین کمیت جالبی است و قانون دوم هم اینچنین قانون شاخصی میباشد. آنچه ما میبینیم این است که دلیل همه اینها قضیه لیوول است. اگر قضیه لیوولی نباشد پارادوکسی هم وجود ندارد!
و این درست همانجایی است که آشوب به میان میآید و میخواهد این پارادوکس را رفع کند. درست است که مقدار عددی حجم کاملاً ثابت باقی میماند اما بر اساس آشوب، شکل آن به شدت تغییر میکند. در برخی جهات کش میآید و در جهاتی دیگر منقبض میشود. مکرراً تا میخورد (موضوع کشآوردن و تا خوردن را به یاد بیاورید). هر نقطهای درون حجم سعی میکند ترژکتوری خود را طی کند، اما ترژکتوریهایی که در ابتدا در همسایگی یکدیگر بودند نهایتاً به صورت نمایی از یکدیگر فاصله میگیرند (حساسیت به شرایط اولیه). پیچکهای جدیدی نمایان میشوند و به هر سو قد میکشند. انواع گرهها شکل میگیرند و پیچیده و پیچیدهتر شده و ساختار، ظریف و ظریفتر میشود. اشل مبنایی ما نیز کوچک و کوچکتر میگردد و شما شاهد شکلگیری یک فرکتال هستید. در محدوده زمانی بسیار بزرگ، آنچه به دست میآورید این است: یک فرکتال.

شکل ۴: تکامل زمانی یک ناحیه ساده از فضای فازی که
تبدیل به یک فرکتال میشود.
اما وضعیت آنتروپی به چه صورت خواهد بود؟ بله، مقدار حجم، همانطور که به وسیله قضیه لیوول تضمین شده بود، ثابت باقی میماند. ولی مشاهده آن حجم، دنبال کردن تغییرات آن، و اندازه گیری آن، به مرور در حال سختتر شدن است (شکل ۴ را مشاهده کنید). به یاد داشته باشید آنچه در اینجا در حال مشاهده کردن آن هستید نمایشی از دانش شما درباره حالت سیستم است. همچنانکه شاهد این هستید که آن حجم بیشتر و بیشتر فرکتالی میشود، حس میکنید دانشتان به تدریج در حال محو شدن است و بیش از این نمیتواند در سر شما قرار گیرد! نهایتاً در حالیکه شاهد آن هستید که دانش گهربارتان بیشتر و بیشتر شبیه توپی پشمی میشود که گربهای در حال رسیدن به خدمتش میباشد، دستهای خود را مایوسانه بالا میبرید و میگویید: «دیگر صبر و تحمل این را ندارم؛ همین الان یک کیسه گرد و صاف و خوشگل دور کل این به هم ریختگی و افتضاح میکشم.» (شکل ۵ را ببینید).

شکل ۵: کیسه کردن به هم ریختگی.
چه شد که یکباره این همه زلمزیمبو به وجود آمد؟ این همه طوفان و رعد و برق برای چیست؟ چه کار کردید؟ شما آنتروپی را افزایش دادید! بله، شما حجم اولیه را با حجمی بزرگتر جایگزین کردید. حجم اولیه پر از سوراخ و حفره بود (یک فرکتال بود). شما آن را با حجمی صاف و بدون سوراخ، و در نتیجه بزرگتر، عوض کردید. و آنتروپی لگاریتم این حجم است: شما همین الان قانون دوم ترمودینامیک را ارضا کردید!
بنابراین این شما هستید که آنتروپی را افزایش دادید. فیزیک این کار را نکرده است، کار آشوب هم نیست، لیوول هم این کار را نکرد: شما خطی صاف و تمیز دور حجم مورد نظر ترسیم کردید تا کارتان سادهتر شود. کار کار خودتان است. آشوب فرکتال را تولید کرد، اما این شما بودید که خواستید آن را صاف و تمیز کنید.
البته افزایش آنتروپی الزاما بصورت ناگهانی یا چشمگیر اتفاق نمیافتد. باید چیزها را بتوان به گونهای تعریف کرد که به صورت هموار و به تدریج افزایش یابد. فرآیندی تحت عنوان درشتبندی کردن[44] وجود دارد که درست همین کار را میکند. در اصل، درشتبندی کردن میگوید قبل از هر بار که میخواهید آنتروپی را حساب کنید باید جزئيات توزیع را برای تمام مقیاسهای کوچکتر از یک اندازه ثابت، صاف و گرد کنید. اندازهای که فراتر از آن قادر نخواهید بود جزئیات را مشاهده کنید. هر سری از این گونه گرد کردنها برابر است با از دست دادن دانش و افزایش حجم موثر توزیع و در نتیجه افزایش آنتروپی.
نتیجه این است که آنتروپیِ بیبعدِ ما، که کمبود دانش ما را اندازهگیری میکند، معیاری کاملاً سابجکتیو (شخصی) میباشد و هیچ ربطی به قوانین بنیادی ذرات و تعاملاتشان ندارد. بلکه درباره این حقیقت است که آشوب چیزها را به هم میریزد؛ به عبارتی در موقعیتهایی که در ابتدا دانستن جزئیاتشان ساده و راحت بود، نهایتاً به لطف آشوب چنان پیچیده میشوند که مجبور خواهیم شد از تلاش برای دانستنشان دست بکشیم.
و یک سوال پایانی: اگر آنتروپی به واقع کاملاً سابجکتیو است، پس چرا برای اکثر مردم، خیلی هم آبجکتیو (عینی) به نظر میآید؟ از هر فیزیک-شیمیدانی که بپرسید به شما میگوید آنتروپی یک ویژگی بنیادی و دائمی ماده به صورت فلهای[45] است. شما میتوانید آن را اندازه بگیرید و با دقت بالا آن را محاسبه کنید، میتوانید در جداول جستجویش کنید و غیره. و پاسخشان به پارادوکس جدید این است: اعداد بزرگ. مشهور است که اعداد بسیار بزرگ، راهی برای تبدیل احتمالات به قطعیت مطلق دارند. ولی ادا شدن حق مطلب، مقاله دیگری را میطلبد.
تقدیر و تشکر
من در اینجا از یانیر بار-یام برای تدریس سیستمهای پیچیده به من و دیگران تشکر میکنم. قدردان کنستانتینو تسالیس برای غنا بخشیدن به مباحثات و کمکهای دیگر او هستم. ویراستار متعهد من، مارتی استاک، نصایح بسیار ارزشمندی در اختیار من گذاشت. بخشی از حمایت مالی این مقاله ذیل قراردادی با دپارتمان انرژی امریکا بوده است.
برای افراد فنیتر، چند کتاب خوب را معرفی میکنم:
Steven H. Strogatz, Nonlinear Dynamics and Chaos (Addison-Wesley, Reading, 1994).
Undergraduate level. Mostly about dissipative chaos. Quite entertaining.
L.E. Reichl, The Transition to Chaos, (Springer, New York, 1992).
Graduate level. Mostly about conservative chaos. Very complete. Includes quantum chaos.
Yaneer Bar-Yam, Dynamics of Complex Systems (Addison-Wesley, Reading, 1997).
Invaluable. Very wide range of topics.
Roger Balian, From Microphysics to Macrophysics, 2 volumes (Springer, Berlin, 1991–2).
A thorough introduction to statistical mechanics.
[1] Michel Baranger
[2] Calculus
[3] “going to the limit”
[4] Continuity
[5] Analyticity
[6] Analysis
[7] Quantitative science
[8] Cantor set
[9] Sierpinski
[10] Mandelbrot
[11] Sonoran Desert
[12] Configuration
[13] Dynamical system
[14] Phase space
[15] Trajectory
[16] Orbit
[17] Edward Lorenz
[18] Integrability
[19] Multiperiodic
[20] Map
[21] Stretching and folding
[22] Croissant, شیرینی هلالی شکل، پچ پچ
[23] Biological
[24] Interdependence
[25] Emerging behavior
[26] Emergence
[27] Self-organization
[28] Adaptive
[29] Self-reproducing
[30] Cooperation
[31] Competition
[32] Jane Austen
[33] Honoré de Balzac
[34] The survival of the fittest
[35] Statistical Mechanics
[36] Disorder
[37] The paradox of the arrow of time
[38] Nicolai Krylov
[39] Dissipative chaos
[40] Strange attractors
[41] Conservative
[42] Special symplectic geometry
[43] Liouville’s theorem
[44] Coarse-graining
[45] matter in bulk